In a recent post, I mentioned that I was testing the stability of clusters generated from a modified network partitioning algorithm using bootstrap resampling techniques. I also mentioned that I was doing this in R, using the very nice foreach package published by REvolution Computing. To show just how nice this package is, below is a minimal example of bootstrapping a network partitioning algorithm which takes advantage of a multicore processor:
library(doMC)
library(foreach)
library(igraph)
# Jaccard coeficcient function (taken from package fpc)
clujaccard = function (c1, c2, zerobyzero = NA) {
if (sum(c1) + sum(c2) - sum(c1 & c2) == 0)
out = zerobyzero
else
out = sum(c1 & c2)/(sum(c1) + sum(c2) - sum(c1 & c2))
return(out)
}
registerDoMC() # registers the parallel backend
B = 1000 # number of bootstrap replicates to create
load("igraph_network.Rdata") # load a previously saved network (network name: g)
fg = fastgreedy.community(g) # compute original clustering
mm = which.max(fg$modularity) # find level of max modularity
moc = community.to.membership(g, fg$merges, mm)$membership # get membership
noc = length(unique(moc)) # count the number original clusters
bg = g # make a copy of g for bootstrapping
clusters = foreach(i=seq(B), .combine=cbind) %dopar% {
E(bg)$weight = sample(E(g)$weight, replace=TRUE) # resample the edge weights
fg = fastgreedy.community(bg) # compute bootstrap clustering
mm = which.max(fg$modularity) # find level of max modularity
mbc = community.to.membership(bg, fg$merges, mm)$membership # get membership
nbc = length(unique(mbc)) # count the number new clusters
bootresult = c()
for (j in seq(0, noc-1)) { # for each of the original clusters...
maxgamma = 0
if (nbc > 0) {
for (k in seq(0, nbc-1)) { # for each of the new clusters...
bv = as.vector(mbc == k)
ov = as.vector(moc == j)
jc = clujaccard(ov, bv, zerobyzero=0)
if (jc > maxgamma) # if these two clusters are most similar...
maxgamma = jc
}
}
bootresult = c(bootresult, maxgamma) # combine results
}
return bootresult # return the results of this iteration (and cbind with the rest)
}
bootmean = apply(clusters, 1, mean) # mean Jaccard coefficient for each cluster
The above example might not produce great results, as it simply
resamples (with replacement) the weights of all the network edges, and
therefore a more sophisticated resampling regime might be warranted.
Having said that, it’s quite a useful example, and as you can see, the
only ‘extra’ bits required to make this run on multiple cores is the
registerDoMC() command which simply registers the parallel backend
(uses the multicore package) and the foreach ... %dopar% which tells R
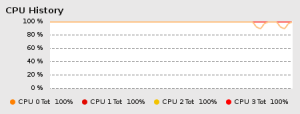
to run the loops in parallel. I ran a similar analysis using a different
community detection algorithm on a computer with 4 cores, and was
(finally) able to take full advantage of my processing power:
Bootstrapping Cluster Networks R FOSS How-To Networks Research