In my last post, I implemented several classification algorithms for quantitative data which could be used directly from the Python console in QGIS. While this was a handy addition to my PyQGIS toolkit, it wasn’t quite handy enough for me, so I decided to (re)implement the same algorithms in C++ so that they could be added directly to the QGIS API. Before I did that however, I wanted to fix a few issues, and speed things up a bit, particularly for the Jenks Natural Breaks algorithm, which can be quite slow for large datasets.
After porting everything over to C++, I noticed that things were still
a little too slow for large datasets. My first thought was to limit the
amount of data that the algorithm had to go through by taking a random
sample (without replacement) and only running the algorithm on this
sample. Based on trial and error, I found that about 1000 values was a
good number to use, as it was still relatively fast, but generally not
too small to be unrepresentative of the overall distribution. In the
end, I went with using max(1000, n*0.10) for layers with more than
1000 features.
Since several of my colleagues here still use ESRI products, I also decided to compare my version with the Natural Breaks algorithm in ArcMAP. I noticed right away that their version was much faster (when I didn’t use the random sampling scheme), so I decided to search around for information on their implementation. Obviously ESRI’s documentation didn’t explain the specifics of their algorithm, but it does produce very similar class breaks to mine (and the implementation available in R, so I was relatively confident that the main underlying algorithm was similar. I then stumbled upon this question in an ESRI forum:
Does ArcMap use the Jenks-Caspall or the Fisher-Jenks algorithm for classifying data into natural breaks. I did some support.esri.com research and found that ArcView 3.x appeared to have used the Fisher-Jenks, but ArcGIS Desktop only generically talked about Jenks Optimization without eluded to what algorithm it was using.
The initial response was quite good, but unfortunately, like all propriety software companies, when asked exactly how the algorithm was implemented, they responded with:
That’s proprietary information, along the lines of a trade secret, and so corporate policy is that we do not provide it.
Bummer… I was able to figure out a few things from simply clicking
around the various different options in ArcMAP, and I found that for
large datasets, ArcMAP’s version of the Jenks algorithm also uses
sampling to reduce computation time. However, I was surprised to find
that their sampling technique appears to simply sample the first x
data values (where x defaults to 10,000, but can be changed by the
user). Depending on how the data was created/digitised, this may not
produce a statistically representative sample at all! In my opinion, it
is better to use a random sampling scheme, with the constraint that both
the minimum and maximum values are included in the random sample so that
we don’t lose values off the ends of our class intervals. Which is
exactly what I’ve done…
At the moment I’m still looking at ways to optimize my rather basic implementation. So far I use a relatively simple sampling procedure, but it might be possible to do something more ‘intelligent’ here to speed things up while maintaining a statistically representative sample. Comments are more than welcome. I have also posted the diff file to the QGIS developers mailing list for evaluation, and once I tidy up a few issues I’ll commit to this trunk, making it available for future versions of QGIS.
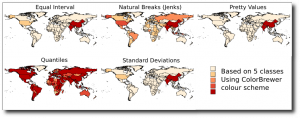
Just to remind you of how important it is to carefully consider the classification scheme you use when presenting your data, here is a graphic of the 5 different classification schemes (soon to be) available in QGIS. All 5 methods are grouping the same underlying data (2007 population) into the same number of classes (5).